Pemakaian tree structure dalam proses pencarian (search)
- Sifat Binary Tree:
Pada sebuah node x,
1. elemen yang berada di LEFT sub-tree selalu lebih KECILdaripada x
2. elemen yang berada di RIGHT sub-tree selalu lebih BESAR Atau SAMA DENGAN daripada x
- Binary Search Tree: proses pencarian (SEARCHING) berbasis binary tree
Tree traversal adalah cara kunjungan node-node pada pohon biner. Ada tiga cara
kunjungan dalam tree:
• Pre-order
• In-order
• Post-order
1. Pre-order
a. Cetak data pada root
b. Secara rekursif mencetak seluruh data pada subpohon kiri
c. Secara rekursif mencetak seluruh data pada subpohon kanan
2. In-order
a. Secara rekursif mencetak seluruh data pada subpohon kiri
b. Cetak data pada root
c. Secara rekursif mencetak seluruh data pada subpohon kanan
3. Post-order
a. Secara rekursif mencetak seluruh data pada subpohon kiri
b. Secara rekursif mencetak seluruh data pada subpohon kanan
c. Cetak data pada root
Contoh notasi matematika, misalkan suatu ekspresi berikut: 3 + 2 * 5 – 4
Sintaks progran pencarian data di Tree
Keterangan :
1. Bandingkan 9 dengan 15; mengujungi kiri
2. Bandingkan 9 dengan 6; mengunjungi kanan
3. Bandingkan 9 dengan 7; mengunjungi kanan
4. Bandingkan 9 dengan 13; mengunjungi kiri
5. Bandingkan 9 dengan 9; data ditemukan
Contoh : Mencari nilai 9
Penghitungan jumlah node dalam tree
Penghitungan kedalaman tree
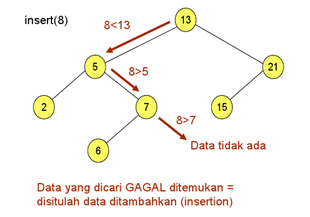
Insert BST
Penyisipan sebuah node baru, didahului dengan operasi pencarian posisi yang sesuai. Dalam hal ini node baru tersebut akan menjadi daun/leaf.
Delete BST
Operasi delete memiliki 3 kemungkinan :
- Delete terhadap node tanpa anak/child (leaf/daun) : node dapat langsung dihapus
- Delete terhadap node dengan satu anak/child : maka node anak akan menggantikan posisinya.
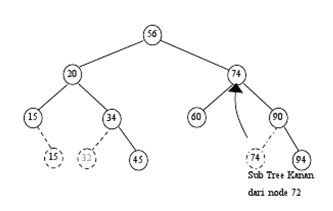
- Delete terhadap node dengan dua anak/child : maka node akan digantikan oleh node paling kiri dari Sub Tree Kanan atau dapat juga digantikan oleh anak paling kanan dari Sub Tree Kiri.
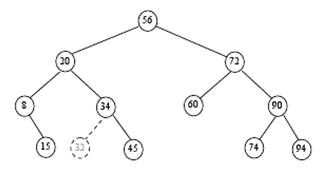
Misalnya ingin dihapus
1. Node (32) : dapat langsung dihapus sehingga akan dihasilkan tree sbb.
2. Node (8) : node dengan satu child
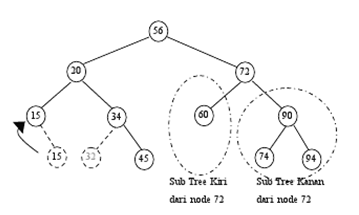
3. Node (72) : node dengan 2 child
Node akan digantikan oleh anak paling kanan dari Sub Tree Kiri (node(60))
Atau anak paling kiri dari Sub Tree Kanan (node(74))
Atau
Syntax Program
//header file
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
//pendeklarasian struct sebuah tree awal
typedef struct Node
{
char data;
Node *kiri;
Node *kanan;
}root; //tipe data abstrak
//fungsi untuk menambahkan node baru
void tambah (Node **root, char databaru)
{
//jika root masih kosong
if ((*root)==NULL)
{
//pembuatan node baru
Node *baru;
//pengalokasian memori dari node yang telah dibuat
baru = new Node;
//inisialisasi awal node yang baru dibuat
baru->data=databaru;
baru->kiri=NULL;
baru->kanan=NULL;
(*root) = baru;
(*root) -> kiri = NULL;
(*root) -> kanan = NULL;
//jika menujuk menunjuk ke NULL artinya tidak mempunyai child
printf("Data Bertambah!");
}
//jika data yang akan dimasukkan lebih kecil daripada elemen root, maka akan diletakkan di node sebelah kiri.
else if (databaru<(*root)->data)
tambah(&(*root)->kiri,databaru);
//jika data yang akan dimasukkan lebih besar daripada elemen root, maka akan diletakkan di node sebelah kanan
else if (databaru>(*root)->data)
tambah(&(*root)->kanan,databaru);
//jika saat dicek data yang akan dimasukkan memiliki nilai yang sama dengan data pada root
else if (databaru==(*root)->data)
printf("Data Sudah ada!");
}
//fungsi yang digunakan untuk mencetak tree secara preOrder
void preOrder(Node *root)
{
if(root!=NULL)
{
if(root->data!=NULL)
{
printf("%c ",root->data);
}
preOrder(root->kiri);
preOrder(root->kanan);
}
}
//fungsi yang digunakan untuk mencetak tree secara inOrder
void inOrder(Node *root)
{
if(root!=NULL)
{
inOrder(root->kiri);
if(root->data!=NULL)
{
printf("%c ",root->data);
}
inOrder(root->kanan);
}
}
//fungsi yang digunakan untuk mencetak tree secara postOrder
void postOrder(Node *root)
{
if(root!=NULL)
{
postOrder(root->kiri);
postOrder(root->kanan);
if(root->data!=NULL)
{
printf("%c ",root->data);
}
}
}
//fungsi yang digunakan untuk melakukan pencarian data
void search(Node **root, int cari)
{
if((*root) == NULL)
{
printf("Data tidak ditemukan!");
}
//jika data yang dicari lebih kecil dari isi root
else if(cari < (*root)->data)
search(&(*root)->kiri,cari);
//jika data yang dicari lebih besar dari isi root
else if(cari > (*root)->data)
search(&(*root)->kanan,cari);
//jika data yang dicari sama dengan isi dari variabel root
else if(cari == (*root)->data)
printf("Data ditemukan!");
}
//fungsi yang digunakan untuk menghapus suatu node
void hapus(Node **root, int del)
{
Node *bantu;
if((*root) == NULL){
printf("tidak ada data");
}
//jika nilai data yang ingin dihapus memiliki nilai sama dengan isi root
else if(del == (*root)->data){
if((*root)->kiri == NULL && (*root)->kanan == NULL){
(*root)=NULL;
printf("Data dihapus!");
}
else{
bantu=(*root)->kanan;
do{
if(bantu->kiri!=NULL){
bantu=bantu->kiri;
}
else if(bantu->kanan!=NULL)
{
bantu=bantu->kanan;
}
}while(bantu->kanan!=NULL || bantu->kiri!=NULL);
(*root)->data=bantu->data;
hapus(&((*root)->kanan),bantu->data);
}
}
//jika nilai data yang ingin dihapus memiliki nilai lebih kecil dari isi root
else if(del < (*root)->data)
hapus(&(*root)->kiri,del);
//jika nilai data yang ingin dihapus memiliki nilai lebih besar dari isi root
else if(del > (*root)->data)
hapus(&(*root)->kanan,del);
}
//fungsi untuk mengetahui jmlah node dalam tree
int count(Node *root)
{
if(root==NULL)
return 0;
else
return count(root->kiri)+ count(root->kanan)+1;
}
//Fungsi untuk mengetahui ketinggian
int height(Node *root){
if(root == NULL)
return -1;
else{
int u = height(root->kiri);
int v = height(root->kanan);
if(u > v)
return u + 1;
else
return v + 1;
}
}
//fungsi utama
int main()
{
//deklarasikan variabel
char pil,del,cari;
Node *pohon;
pohon = NULL; //inisialisasi node pohon
while (true)
{
system("cls"); //bersihkan layar
char data;
printf("\t#PROGRAM TREE C++#");
printf("\n\t==================");
printf("\nMENU");
printf("\n----\n");
printf("[1] Tambah Data\n");
printf("[2] Lihat Pre-Order\n");
printf("[3] Lihat In-Order\n");
printf("[4] Lihat Post-Order\n");
printf("[5] Delete\n");
printf("[6] Kosongkan Data\n");
printf("[7] Search\n");
printf("[8] Hitung Node pada Tree\n");
printf("[9] Kedalaman Tree\n");
printf("[X] Keluar\n");
printf("Pilihan Anda : ");
scanf("%c",&pil);
fflush(stdin); //mengosongkan buffering
switch(pil)
{
//jika pil bernilai '1'
case '1':
printf("\nINPUT : ");
printf("\n-------");
printf("\nMasukkan sebuah karakter : ");
scanf("%c", &data);
//panggil fungsi untuk menambah node yang berisi data pada tree
tambah(&pohon,data);
break;
//jika pil bernilai '2'
case '2':
printf("\nOUTPUT PRE ORDER : ");
printf("\n------------------\n");
if(pohon!=NULL)
//panggil fungsi untuk mencetak data secara preOrder
preOrder(pohon);
else
printf("Masih Kosong!!!");
break;
//jika pil bernilai '3'
case '3':
printf("\nOUTPUT IN ORDER : ");
printf("\n------------------\n");
if(pohon!=NULL)
//panggil fungsi untuk mencetak data secara inOrder
inOrder(pohon);
else
printf("Masih Kosong!!!");
break;
//jika pil bernilai '4'
case '4':
printf("\nOUTPUT POST ORDER : ");
printf("\n------------------\n");
if(pohon!=NULL)
//panggil fungsi untuk mencetak data secara postOrder
postOrder(pohon);
else
printf("Masih Kosong!!!");
break;
//jika pil bernilai '5'
case '5':
if(pohon!=NULL)
{
printf("\nSEBELUM NODE DIHAPUS : ");
printf("\n---------------------- ");
//panggil fungsi untuk mencetak data secara preOrder
printf("\nPRE ORDER : ");
preOrder(pohon); //panggil fungsi
printf("\nIN ORDER : ");
inOrder(pohon); //panggil fungsi
printf("\nPOST ORDER : ");
postOrder(pohon); //panggil fungsi
printf("\n\nPENGHAPUSAN DATA : ");
printf("\n------------------\n");
printf("Masukkan data yang ingin dihapus: ");
scanf("%c", &del);
//panggil fungsi yang digunakan untuk melakukan penghapusan pada suatu node
hapus(&pohon, del);
printf("\n\nSETELAH NODE DIHAPUS : ");
printf("\n---------------------- ");
printf("\nPRE ORDER : ");
preOrder(pohon); //panggil fungsi
printf("\nIN ORDER : ");
inOrder(pohon); //panggil fungsi
printf("\nPOST ORDER : ");
postOrder(pohon); //panggil fungsi
}
else
printf("\nMasih kosong!");
break;
//jika pil bernilai '6'
case '6':
pohon=NULL;
printf("\nPENGOSONGAN ELEMEN ");
printf("\n------------------");
printf("\nTree sudah dikosongkan!!");
break;
//jika pil bernilai '7'
case '7':
printf("\nOUTPUT -> Hanya untuk mengecek apakah data dimaksud terdapat dalam tree");
printf("\n------");
if(pohon!=NULL)
{
//panggil fungsi untuk mencetak data secara preOrder
printf("\nPRE ORDER : ");
preOrder(pohon); //panggil fungsi
printf("\nIN ORDER : ");
inOrder(pohon); //panggil fungsi
printf("\nPOST ORDER : ");
postOrder(pohon); //panggil fungsi
printf("\n\nPENCARIAN DATA");
printf("\n--------------");
printf("\nMasukkan data yang ingin dicari : ");
scanf("%c", &cari);
//panggil fungsi untuk melakukan pencarian data pada tree
search(&pohon, cari);
}
else
printf("\nMasih kosong!");
break;
//jika pil bernilai '8'
case '8':
printf("\nJUMLAH NODE DI DALAM TREE");
printf("\n-------------------------");
printf("\nJumlah Node : %d", count(pohon));
getch();
break;
//jika pil bernilai '9'
case '9' :
printf("\nKEDALAMAN TREE(LEVEL-> DIMULAI DARI 0)");
printf("\n----------------------------------------");
printf("\nKedalaman tree : %d\n", height(pohon));
break;
//jika pil bernilai 'X' atau 'x'
case 'X'|'x':
exit(0);
break;
}
_getch();
}
}
Penjelasan :
· Pada Program ini dideklarasikan beberapa fungsi untuk melakukan operasi pada Tree, fungsi tersebut antara lain :
o void search(Node **root, int cari)
o void postOrder(Node *root)
o void inOrder(Node *root)
o void preOrder(Node *root)
o void tambah (Node **root, char databaru)
o int height(Node *root)
o int count(Node *root)
o void hapus(Node **root, int del)
· Pada posting ini hanya akan dijelaskan beberapa fungsi yang belum pernah dibahas pada posting sebelumnya. Fungsi tersebut adalah
Hitung jumlah node dalam tree
int count(Node *root)
{
if(root==NULL)
return 0;
else
return count(root->kiri)+ count(root->kanan)+1;
}
Jika root bernilai NULL, Artinya tree masih kosong, maka akan memberikan nilai balik berupa 0. Sebaliknya, jika root tidak bernilai NULL maka penghitungan jumlah node dalam tree dilakukan dengan cara mengunjungi setiap node, dimulai dari root ke subtree kiri, kemudian ke subtree kanan dan masing-masing node dicatat jumlahnya, dan terakhir jumlah node yang ada di subtree kiri dijumlahkan dengan jumlah node yang ada di subtree kanan ditambah 1 yaitu node root.
Hitung kedalaman tree
int height(Node *root){
if(root == NULL)
return -1;
else{
int u = height(root->kiri);
int v = height(root->kanan);
if(u > v)
return u + 1;
else
return v + 1;
}
}
Jika root bernilai NULL, artinya tree masih kosong, maka akan memberikan nilai balik berupa -1.Sebaliknya, jika root tidak bernilai NULL maka penghitungan kedalaman dihitung dari setelah root, yang dimulai dari subtree bagian kiri kemudian ke subtree bagian kanan. Untuk masing-masing kedalaman kiri dan kanan akan dibandingkan, jika ternyata subtree kiri lebih dalam, maka yang dipakai adalah jumlah kedalaman subtree kiri, demikian sebaliknya. Hal ini didasarkan pada prinsip binary tree, dimana tree-nya selalu memiliki maksimal 2 node anak.
Penghapusan Node
Operasi delete memiliki 3 kemungkinan :
- Delete terhadap node tanpa anak/child (leaf/daun) : node dapat langsung dihapus
- Delete terhadap node dengan satu anak/child : maka node anak akan menggantikan posisinya.
- Delete terhadap node dengan dua anak/child : maka node akan digantikan oleh node paling kiri dari Sub Tree Kanan atau dapat juga digantikan oleh anak paling kanan dari Sub Tree Kiri.
Tree sebelum node d dihapus :
Tree setelah node d dihapus :
Perhatikan kondisi ketiga (jika node punya dua anak) maka node (d) akan digantikan oleh node paling kiri dari Sub Tree Kanan (node e) atau dapat juga digantikan oleh anak paling kanan dari Sub Tree Kiri.
Output
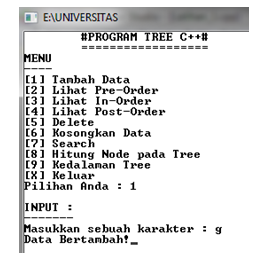
1. Tambah data (Data yang diinput berturut-turut adalah d, b, f, a, c, e, g). Output yang ditampilkan adalah output dari input data terakhir.
2. Lihat pre-order
3. Lihat in-order
4. Lihat post-order
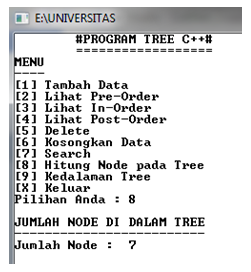
5. Jumlah Node pada Tree
6. Kedalaman(ketinggian) Tree
7. Search node
8. Delete Node
9. Kosongkan Data
10. Exit

.png)




























Tidak ada komentar:
Posting Komentar